n



Next: カオス制御
Up: 研究内容概要
Previous: スイッチのある非線形回路の分岐現象とカオス
Index
物理系の非線形のモデル化と,それらの動的振るまいの
定性的・定量的解析の基礎的手法に関する研究を行なっています.
[68], [71], [], [82], [148],
非線形常微分(差分)方程式で記述される力学系では,
式のパラメータの変化により,周期軌道の位相的性質が変化,
つまり分岐現象が生じ,カオスへと進展します.
パラメータ平面でこれらを求めた分岐図は
力学系の大域的な振るまいの理解,カオスの存在範囲の把握の上で
重要な手がかりとなります.
さまざまな力学系の分岐問題を解き,
その普遍的な性質を見出すことがこのテーマの目的です.
具体的に,区分非線形系の分岐問題の計算は,世界でも
まだウチの研究室以外は計算できないと思います[89][112]
分岐計算の手法の検討や既存アルゴリズムの開発も行なっています.
また力学系に関する種々の情報を計算することも試みられています
[54], [63], [151], [154]
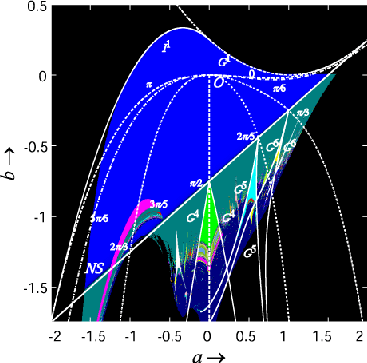
Figure 2:
ある非線形2次写像の分岐図.点線は固定点の特定の
位相に対応する等高線である.
|
|
Contact address: ueta @ tokushima-u.ac.jp